块状链表

./images/kuaizhuanglianbiao.png

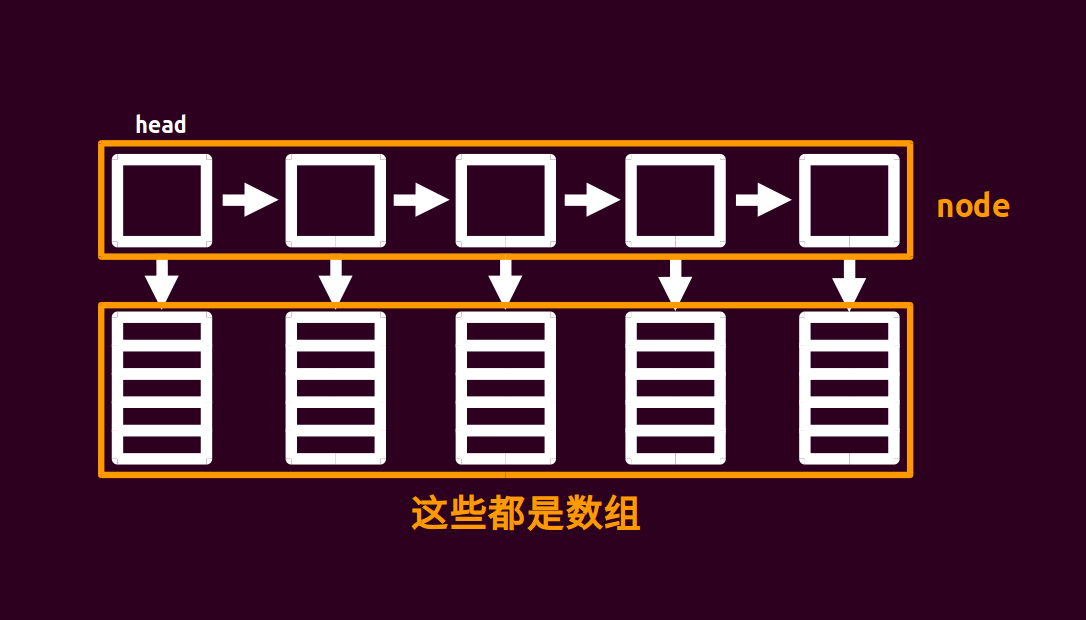
块状链表大概就长这样……

不难发现块状链表就是一个链表，每个节点指向一个数组。我们把原来长度为 n 的数组分为 $\sqrt{n}$ 个节点，每个节点对应的数组大小为 $\sqrt{n}$ 。所以我们这么定义结构体，代码见下。其中 sqn 表示 sqrt(n) 即 $\sqrt{n}$ ，pb 表示 push_back，即在这个 node 中加入一个元素。

实现

struct node {
  node* nxt;
  int size;
  char d[(sqn << 1) + 5];

  node() { size = 0, nxt = NULL, memset(d, 0, sizeof(d)); }

  void pb(char c) { d[size++] = c; }
};

块状链表应该至少支持：分裂、插入、查找。什么是分裂？分裂就是分裂一个 node，变成两个小的 node，以保证每个 node 的大小都接近 $\sqrt{n}$ （否则可能退化成普通数组）。当一个 node 的大小超过 $2\times \sqrt{n}$ 时执行分裂操作。

分裂操作怎么做呢？先新建一个节点，再把被分裂的节点的后 $\sqrt{n}$ 个值 copy 到新节点，然后把被分裂的节点的后 $\sqrt{n}$ 个值删掉（size--），最后把新节点插入到被分裂节点的后面即可。

块状链表的所有操作的复杂度都是 $\sqrt{n}$ 的。

还有一个要说的。随着元素的插入（或删除），会变， $\sqrt{n}$ 也会变。这样块的大小就会变化，我们难道还要每次维护块的大小？

其实不然，把 $\sqrt{n}$ 设置为一个定值即可。比如题目给的范围是，那么 $\sqrt{n}$ 就设置为大小为的常量，不用更改它。

list<vector<char>> orz_list;

STL 中的 `rope`

导入

STL 中的 rope 也起到块状链表的作用，它采用可持久化平衡树实现，可完成随机访问和插入、删除元素的操作。

由于 rope 并不是真正的用块状链表来实现，所以它的时间复杂度并不等同于块状链表，而是相当于可持久化平衡树的复杂度（即 $O(\log n)$ ）。

可以使用如下方法来引入：

#include <ext/rope>
using namespace __gnu_cxx;

关于双下划线开头的库函数

OI 中，关于能否使用双下划线开头的库函数曾经一直不确定，2021 年 CCF 发布的关于 NOI 系列活动中编程语言使用限制的补充说明中提到「允许使用以下划线开头的库函数或宏，但具有明确禁止操作的库函数和宏除外」。故 rope 目前可以在 OI 中正常使用。

基本操作

操作	作用
`rope <int > a`	初始化 `rope`（与 `vector` 等容器很相似）
`a.push_back(x)`	在 `a` 的末尾添加元素 `x`
`a.insert(pos, x)`	在 `a` 的 `pos` 个位置添加元素 `x`
`a.erase(pos, x)`	在 `a` 的 `pos` 个位置删除 `x` 个元素
`a.at(x)` 或 `a[x]`	访问 `a` 的第 `x` 个元素
`a.length()` 或 `a.size()`	获取 `a` 的大小

例题

POJ2887 Big String

题解：很简单的模板题。代码如下：

#include <cctype>
#include <cstring>
#include <iostream>
using namespace std;
constexpr int sqn = 1e3;

struct node {  // 定义块状链表
  node* nxt;
  int size;
  char d[(sqn << 1) + 5];

  node() { size = 0, nxt = NULL; }

  void pb(char c) { d[size++] = c; }
}* head = NULL;

char inits[(int)1e6 + 5];
int llen, q;

void readch(char& ch) {  // 读入字符
  do cin >> ch;
  while (!isalpha(ch));
}

void check(node* p) {  // 判断，记得要分裂
  if (p->size >= (sqn << 1)) {
    node* q = new node;
    for (int i = sqn; i < p->size; i++) q->pb(p->d[i]);
    p->size = sqn, q->nxt = p->nxt, p->nxt = q;
  }
}

void insert(char c, int pos) {  // 元素插入，借助链表来理解
  node* p = head;
  int tot, cnt;
  if (pos > llen++) {
    while (p->nxt != NULL) p = p->nxt;
    p->pb(c), check(p);
    return;
  }
  for (tot = head->size; p != NULL && tot < pos; p = p->nxt, tot += p->size);
  tot -= p->size, cnt = pos - tot - 1;
  for (int i = p->size - 1; i >= cnt; i--) p->d[i + 1] = p->d[i];
  p->d[cnt] = c, p->size++;
  check(p);
}

char query(int pos) {  // 查询
  node* p;
  int tot;
  for (p = head, tot = head->size; p != NULL && tot < pos;
       p = p->nxt, tot += p->size);
  tot -= p->size;
  return p->d[pos - tot - 1];
}

int main() {
  cin.tie(nullptr)->sync_with_stdio(false);
  cin >> inits >> q;
  llen = strlen(inits);
  node* p = new node;
  head = p;
  for (int i = 0; i < llen; i++) {
    if (i % sqn == 0 && i) p->nxt = new node, p = p->nxt;
    p->pb(inits[i]);
  }
  char a;
  int k;
  while (q--) {
    readch(a);
    if (a == 'Q')
      cin >> k, cout << query(k) << '\n';
    else
      readch(a), cin >> k, insert(a, k);
  }
  return 0;
}

本页面最近更新：2024/10/9 22:38:42，更新历史
发现错误？想一起完善？在 GitHub 上编辑此页！
本页面贡献者：HeRaNO, konnyakuxzy, Chrogeek, ChungZH, Enter-tainer, iamtwz, Ir1d, kenlig, ksyx, littlefrog, littlefrogfromthenorth, megakite, shuzhouliu, StudyingFather, Tiphereth-A, Xeonacid
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供，附加条款亦可能应用

块状链表

STL 中的 rope

导入

基本操作

例题

STL 中的 `rope`