支配树 前言 1959 年,「支配」这一概念由 Reese T. Prosser 在 一篇关于网络流的论文 中提出,但并未提出具体的求解算法;直到 1969 年,Edward S. Lowry 和 C. W. Medlock 才首次提出了 有效的求解算法 .而目前使用最为广泛的 Lengauer–Tarjan 算法则由 Lengauer 和 Tarjan 于 1979 年在 一篇论文 中提出.
在 OI 界中,支配树的概念最早在 ZJOI2012 灾难 中被引入,当时也被称为「灭绝树」;陈孙立也在 2020 年的国家集训队论文中介绍了这一算法.
目前支配树在竞赛界并不流行,其相关习题并不多见;但支配树在工业上,尤其是编译器相关领域,已有广泛运用.
本文将介绍支配树的概念及几种求解方法.
支配关系 我们在任意的一个有向图上钦定一个入口结点 𝑠 s 𝑢 u 𝑠 s 𝑢 u 𝑣 v 𝑣 v 支配 𝑢 u 𝑣 v 𝑢 u 支配点 ,记作 𝑣 𝑑 𝑜 𝑚 𝑢 v d o m u
对于从 𝑠 s 𝑠 s
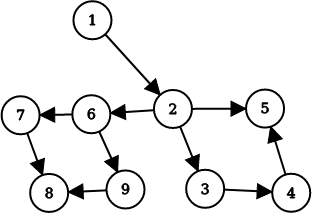
例如这张有向图中,2 2 1 1 3 3 1 , 2 1 , 2 1 , 2 , 3 1 , 2 , 3 1 , 2 1 , 2
引理 在下文的引理中,默认 𝑢 , 𝑣 , 𝑤 ≠ 𝑠 u , v , w ≠ s
引理 1: 𝑠 s
证明: 显然任何一条从 𝑠 s 𝑢 u 𝑠 s 𝑢 u
引理 2: 仅考虑简单路径得出的支配关系与考虑所有路径得出的关系相同.
证明: 对于非简单路径,我们设两次经过某个结点之间经过的所有结点的点集为 𝑆 S 𝑆 S
在 𝑆 S 𝑠 s 𝑢 u
综上,删去非简单路径对支配关系没有影响.
引理 3: 如果 𝑢 u 𝑑 𝑜 𝑚 d o m 𝑣 v 𝑣 v 𝑑 𝑜 𝑚 d o m 𝑤 w 𝑢 u 𝑑 𝑜 𝑚 d o m 𝑤 w
证明: 经过 𝑤 w 𝑣 v 𝑣 v 𝑢 u 𝑤 w 𝑢 u 𝑢 𝑑 𝑜 𝑚 𝑤 u d o m w
引理 4: 如果 𝑢 𝑑 𝑜 𝑚 𝑣 u d o m v 𝑣 𝑑 𝑜 𝑚 𝑢 v d o m u 𝑢 = 𝑣 u = v
证明: 假设 𝑢 ≠ 𝑣 u ≠ v 𝑣 v 𝑢 u 𝑢 u 𝑣 v
引理 5: 若 𝑢 ≠ 𝑣 ≠ 𝑤 u ≠ v ≠ w 𝑢 𝑑 𝑜 𝑚 𝑤 u d o m w 𝑣 𝑑 𝑜 𝑚 𝑤 v d o m w 𝑢 𝑑 𝑜 𝑚 𝑣 u d o m v 𝑣 𝑑 𝑜 𝑚 𝑢 v d o m u
证明: 考虑一条 𝑠 → ⋯ → 𝑢 → ⋯ → 𝑣 → ⋯ → 𝑤 s → ⋯ → u → ⋯ → v → ⋯ → w 𝑢 u 𝑣 v 𝑢 u 𝑠 s 𝑣 v 𝑠 → ⋯ → 𝑣 → ⋯ → 𝑤 s → ⋯ → v → ⋯ → w 𝑢 𝑑 𝑜 𝑚 𝑤 u d o m w
求解支配关系 结点删除法 一个和定义等价的结论:如果我们删去图中的某一个结点后,有一些结点变得不可到达,那么这个被删去的结点支配这些变得不可到达的结点.
因此我们只要尝试将每一个结点删去后 dfs 即可,代码复杂度为 𝑂 ( 𝑛 3 ) O ( n 3 )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26 // 假设图中有 n 个结点, 起始点 s = 1
std :: bitset < N > vis ;
std :: vector < int > edge [ N ];
std :: vector < int > dom [ N ];
void dfs ( int u , int del ) {
vis [ u ] = true ;
for ( int v : edge [ u ]) {
if ( v == del or vis [ v ]) {
continue ;
}
dfs ( v , del );
}
}
void getdom () {
for ( int i = 2 ; i <= n ; ++ i ) {
vis . reset ();
dfs ( 1 , i );
for ( int j = 1 ; j <= n ; ++ j ) {
if ( ! vis [ j ]) {
dom [ j ]. push_back ( i );
}
}
}
}
数据流迭代法 数据流迭代法也是 OI 中不常见的一个知识点,这里先做简要介绍.
数据流分析是编译原理中的概念,用于分析数据如何在程序执行路径上的流动;而数据流迭代法是在程序的流程图的结点上列出方程并不断迭代求解,从而求得程序的某些点的数据流值的一种方法.这里我们就是把有向图看成了一个程序流程图.
这个问题中,方程为:
𝑑 𝑜 𝑚 ( 𝑢 ) = { 𝑢 } ∪ ⎛ ⎜ ⎜ ⎝ ⋂ 𝑣 ∈ 𝑝 𝑟 𝑒 ( 𝑢 ) 𝑑 𝑜 𝑚 ( 𝑣 ) ⎞ ⎟ ⎟ ⎠ d o m ( u ) = { u } ∪ ( ⋂ v ∈ p r e ( u ) d o m ( v ) ) 其中 𝑝 𝑟 𝑒 ( 𝑢 ) p r e ( u ) 𝑢 u
翻译成人话就是,一个点的支配点的点集为它所有前驱结点的支配点集的交集,再并上它本身.根据这个方程将每个结点上的支配点集不断迭代直至答案不变即可.
为了提高效率,我们希望每轮迭代时,当前迭代的结点的所有前驱结点尽可能都已经执行完了这次迭代,因此我们要利用深度优先排序得出这个图的逆后序,根据这个顺序进行迭代.
下面给出核心代码的参考实现.这里需要预先处理每个点的前驱结点集和图的逆后序,但这不是本文讨论的主要内容,故这里不提供参考实现.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30 std :: vector < int > pre [ N ]; // 每个结点的前驱结点
std :: vector < int > ord ; // 图的逆后序
std :: bitset < N > dom [ N ];
std :: vector < int > Dom [ N ];
void getdom () {
dom [ 1 ][ 1 ] = true ;
flag = true ;
while ( flag ) {
flag = false ;
for ( int u : ord ) {
std :: bitset < N > tmp ;
tmp [ u ] = true ;
for ( int v : pre [ u ]) {
tmp &= dom [ v ];
}
if ( tmp != dom [ u ]) {
dom [ u ] = tmp ;
flag = true ;
}
}
}
for ( int i = 2 ; i <= n ; ++ i ) {
for ( int j = 1 ; j <= n ; ++ j ) {
if ( dom [ i ][ j ]) {
Dom [ i ]. push_back ( j );
}
}
}
}
不难看出上述算法的复杂度为 𝑂 ( 𝑛 2 ) O ( n 2 )
支配树 上一节我们发现,除 𝑠 s 𝑠 s
我们将任意一个结点 𝑢 u 𝑣 v 𝑢 u 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) = 𝑣 i d o m ( u ) = v 𝑠 s
我们考虑对于除 𝑠 s 𝑢 u 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) 𝑢 u 𝑛 n 𝑛 − 1 n − 1 支配树 .
求解支配树 根据 dom 求解 不妨考虑某个结点的支配点集 { 𝑠 1 , 𝑠 2 , … , 𝑠 𝑘 } { s 1 , s 2 , … , s k } 𝑠 → ⋯ → 𝑠 1 → ⋯ → 𝑠 2 → ⋯ → ⋯ → 𝑠 𝑘 → ⋯ → 𝑢 s → ⋯ → s 1 → ⋯ → s 2 → ⋯ → ⋯ → s k → ⋯ → u 𝑢 u 𝑠 𝑘 s k
对于一个结点 𝑢 u 𝑆 S 𝑣 ∈ 𝑆 v ∈ S ∀ 𝑤 ∈ 𝑆 ∖ { 𝑢 , 𝑣 } , 𝑤 𝑑 𝑜 𝑚 𝑣 ∀ w ∈ S ∖ { u , v } , w d o m v 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) = 𝑣 i d o m ( u ) = v
因此,利用前文所述的算法得到每个结点的支配点集之后,我们根据上述定义便能很轻松地得到每个点的直接支配点,从而构造出支配树.下面给出参考代码.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18 std :: bitset < N > dom [ N ];
std :: vector < int > Dom [ N ];
int idom [ N ];
void getidom () {
for ( int u = 2 ; u <= n ; ++ u ) {
for ( int v : Dom [ u ]) {
std :: bitset < N > tmp = ( dom [ v ] & dom [ u ]) ^ dom [ u ];
if ( tmp . count () == 1 and tmp [ u ]) {
idom [ u ] = v ;
break ;
}
}
}
for ( int u = 2 ; u <= n ; ++ u ) {
e [ idom [ u ]]. push_back ( u );
}
}
树上的特例 显然树型图的支配树就是它本身.
DAG 上的特例 我们发现 DAG 有一个很好的性质:根据拓扑序求解,先求得的解不会对后续的解产生影响.我们可以利用这个特点快速求得 DAG 的支配树.
提醒 值得注意的是此处的 DAG 只能有一个起点,如果有多个起点,受起点支配的点在支配树上出现有多个父亲的情况,从而使支配关系不能简单的用支配树来表达.
引理 6: 在有向图上,𝑣 𝑑 𝑜 𝑚 𝑢 v d o m u ∀ 𝑤 ∈ 𝑝 𝑟 𝑒 ( 𝑢 ) , 𝑣 𝑑 𝑜 𝑚 𝑤 ∀ w ∈ p r e ( u ) , v d o m w
证明: 首先来证明充分性.考虑任意一条从 𝑠 s 𝑢 u 𝑤 ∈ 𝑝 𝑟 𝑒 ( 𝑢 ) w ∈ p r e ( u ) 𝑣 v 𝑠 s 𝑢 u 𝑣 v 𝑣 𝑑 𝑜 𝑚 𝑢 v d o m u
然后是必要性.如果 ∃ 𝑤 ∈ 𝑝 𝑟 𝑒 ( 𝑢 ) ∃ w ∈ p r e ( u ) 𝑣 v 𝑤 w 𝑣 v 𝑠 → ⋯ → 𝑤 → ⋯ → 𝑢 s → ⋯ → w → ⋯ → u 𝑣 v 𝑢 u
我们发现,𝑢 u 𝑢 u
下面给出参考实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61 std :: stack < int > sta ;
std :: vector < int > e [ N ], g [ N ], tree [ N ]; // g 是原图的反图,tree 是支配树
int n , s , in [ N ], tpn [ N ], dep [ N ], idom [ N ]; // n 为总点数,s 为起始点,in 为入度
int fth [ N ][ 17 ];
void topo ( int s ) {
sta . push ( s );
while ( ! sta . empty ()) {
int u = sta . top ();
sta . pop ();
tpn [ ++ tot ] = u ;
for ( int v : e [ u ]) {
-- in [ v ];
if ( ! in [ v ]) {
sta . push ( v );
}
}
}
}
int lca ( int u , int v ) {
if ( dep [ u ] < dep [ v ]) {
std :: swap ( u , v );
}
for ( int i = 15 ; i >= 0 ; -- i ) {
if ( dep [ fth [ u ][ i ]] >= dep [ v ]) {
u = fth [ u ][ i ];
}
}
if ( u == v ) {
return u ;
}
for ( int i = 15 ; i >= 0 ; -- i ) {
if ( fth [ u ][ i ] != fth [ v ][ i ]) {
u = fth [ u ][ i ];
v = fth [ v ][ i ];
}
}
return fth [ u ][ 0 ];
}
void build () {
topo ( s );
for ( int i = 1 ; i <= n ; ++ i )
for ( int j = 0 ; j <= 15 ; ++ j ) fth [ i ][ j ] = s ;
for ( int i = 1 ; i <= n ; ++ i ) {
int u = tpn [ i ];
if ( g [ u ]. size ()) {
int v = g [ u ][ 0 ];
for ( int j = 1 , q = g [ u ]. size (); j < q ; ++ j ) {
v = lca ( v , g [ u ][ j ]);
}
tree [ v ]. push_back ( u );
fth [ u ][ 0 ] = v ;
dep [ u ] = dep [ v ] + 1 ;
for ( int i = 1 ; i <= 15 ; ++ i ) {
fth [ u ][ i ] = fth [ fth [ u ][ i - 1 ]][ i - 1 ];
}
}
}
}
Lengauer–Tarjan 算法 Lengauer–Tarjan 算法是求解支配树最有名的算法之一,可以在 𝑂 ( 𝑛 𝛼 ( 𝑛 , 𝑚 ) ) O ( n α ( n , m ) ) 半支配点 的概念,并通过半支配点辅助求得直接支配点.
约定 首先,我们从 𝑠 s 𝑇 T 𝑑 𝑓 𝑛 ( 𝑢 ) d f n ( u ) 𝑢 u 𝑢 < 𝑣 u < v 𝑑 𝑓 𝑛 ( 𝑢 ) < 𝑑 𝑓 𝑛 ( 𝑣 ) d f n ( u ) < d f n ( v )
半支配点 一个结点 𝑢 u 𝑣 v 𝑢 , 𝑣 u , v 𝑢 u 𝑢 u 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u )
𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) = m i n ( 𝑣 | ∃ 𝑣 = 𝑣 0 → 𝑣 1 → ⋯ → 𝑣 𝑘 = 𝑢 , ∀ 1 ≤ 𝑖 ≤ 𝑘 − 1 , 𝑣 𝑖 > 𝑢 ) s d o m ( u ) = min ( v | ∃ v = v 0 → v 1 → ⋯ → v k = u , ∀ 1 ≤ i ≤ k − 1 , v i > u )
我们发现半支配点有一些有用的性质:
引理 7: 对于任意结点 𝑢 u 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) < 𝑢 s d o m ( u ) < u
证明: 根据定义不难发现,𝑢 u 𝑇 T 𝑓 𝑎 ( 𝑢 ) f a ( u ) 𝑓 𝑎 ( 𝑢 ) < 𝑢 f a ( u ) < u 𝑢 u
引理 8: 对于任意结点 𝑢 u 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) 𝑇 T
证明: 𝑇 T 𝑠 s 𝑢 u 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u )
引理 9: 对于任意结点 𝑢 u 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑇 T
证明: 假设 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑢 u 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) d f s dfs 𝑢 u 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u )
引理 10: 对于任意结点 𝑢 u 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u )
证明: 考虑可以从 𝑠 s 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑢 u 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑢 u 𝑢 u 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u )
引理 11: 对于任意结点 𝑢 ≠ 𝑣 u ≠ v 𝑣 v 𝑢 u 𝑣 v 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) i d o m ( v )
证明: 对于任意在 𝑣 v 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) i d o m ( v ) 𝑤 w 𝑤 w 𝑠 s 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) i d o m ( v ) 𝑣 v 𝑤 w 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) 𝑣 v 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) i d o m ( v )
根据以上引理,我们可以得到以下定理:
定理 1: 一个点 𝑢 u 𝑇 T 𝑢 u 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) = m i n ( { 𝑣 | ∃ 𝑣 → 𝑢 , 𝑣 < 𝑢 } ∪ { 𝑠 𝑑 𝑜 𝑚 ( 𝑤 ) | 𝑤 > 𝑢 𝑎 𝑛 𝑑 ∃ 𝑤 → ⋯ → 𝑣 → 𝑢 } ) s d o m ( u ) = min ( { v | ∃ v → u , v < u } ∪ { s d o m ( w ) | w > u a n d ∃ w → ⋯ → v → u } )
证明: 令 𝑥 x
我们首先证明 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) ≤ 𝑥 s d o m ( u ) ≤ x 𝑥 x 𝑢 u 𝑥 = 𝑣 0 → ⋯ → 𝑣 𝑗 = 𝑤 x = v 0 → ⋯ → v j = w 𝑇 T ∀ 𝑖 ∈ [ 𝑗 , 𝑘 − 1 ] , 𝑣 𝑖 ≥ 𝑤 > 𝑢 ∀ i ∈ [ j , k − 1 ] , v i ≥ w > u 𝑤 = 𝑣 𝑗 → ⋯ → 𝑣 𝑘 = 𝑣 w = v j → ⋯ → v k = v 𝑣 → 𝑢 v → u
然后我们证明 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) ≥ 𝑥 s d o m ( u ) ≥ x 𝑢 u 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) = 𝑣 0 → 𝑣 1 → ⋯ → 𝑣 𝑘 = 𝑢 s d o m ( u ) = v 0 → v 1 → ⋯ → v k = u 𝑘 = 1 k = 1 𝑘 > 1 k > 1 𝑘 = 1 k = 1 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) → 𝑢 s d o m ( u ) → u 𝑘 > 1 k > 1 𝑗 j 𝑗 ≥ 1 j ≥ 1 𝑣 𝑗 v j 𝑣 𝑘 − 1 v k − 1 𝑇 T 𝑘 k 𝑗 j
考虑证明 𝑣 0 → ⋯ → 𝑣 𝑗 v 0 → ⋯ → v j 𝑣 𝑗 v j ∀ 𝑖 ∈ [ 1 , 𝑗 ) , 𝑣 𝑖 > 𝑣 𝑗 ∀ i ∈ [ 1 , j ) , v i > v j 𝑖 i 𝑣 𝑖 < 𝑣 𝑗 v i < v j 𝑣 𝑖 v i 𝑣 𝑖 v i 𝑣 𝑗 v j 𝑗 j 𝑠 𝑑 𝑜 𝑚 ( 𝑣 𝑗 ) ≤ 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( v j ) ≤ s d o m ( u ) 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) ≤ 𝑥 s d o m ( u ) ≤ x 𝑥 = 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) x = s d o m ( u )
根据定理 1 我们便可以求出每个点的半支配点了.不难发现计算半支配点的复杂度瓶颈在第二种情况上,我们考虑利用带权并查集优化,每次路径压缩时更新最小值即可.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 void dfs ( int u ) {
dfn [ u ] = ++ dfc ;
pos [ dfc ] = u ;
for ( int i = h [ 0 ][ u ]; i ; i = e [ i ]. x ) {
int v = e [ i ]. v ;
if ( ! dfn [ v ]) {
dfs ( v );
fth [ v ] = u ;
}
}
}
int find ( int x ) {
if ( fa [ x ] == x ) {
return x ;
}
int tmp = fa [ x ];
fa [ x ] = find ( fa [ x ]);
if ( dfn [ sdm [ mn [ tmp ]]] < dfn [ sdm [ mn [ x ]]]) {
mn [ x ] = mn [ tmp ];
}
return fa [ x ];
}
void getsdom () {
dfs ( 1 );
for ( int i = 1 ; i <= n ; ++ i ) {
mn [ i ] = fa [ i ] = sdm [ i ] = i ;
}
for ( int i = dfc ; i >= 2 ; -- i ) {
int u = pos [ i ], res = INF ;
for ( int j = h [ 1 ][ u ]; j ; j = e [ j ]. x ) {
int v = e [ j ]. v ;
if ( ! dfn [ v ]) {
continue ;
}
find ( v );
if ( dfn [ v ] < dfn [ u ]) {
res = std :: min ( res , dfn [ v ]);
} else {
res = std :: min ( res , dfn [ sdm [ mn [ v ]]]);
}
}
sdm [ u ] = pos [ res ];
fa [ u ] = fth [ u ];
}
}
求解直接支配点 转化为 DAG 可是我还是不知道半支配点有什么用!
我们考虑在 𝑇 T 𝑢 u 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) → 𝑢 s d o m ( u ) → u 𝐺 G
通过半支配点求解 建一堆图也太不优雅了!
定理 2: 对于任意节点 𝑢 u 𝑇 T 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑤 w 𝑣 v 𝑠 𝑑 𝑜 𝑚 ( 𝑣 ) ≥ 𝑠 𝑑 𝑜 𝑚 ( 𝑤 ) s d o m ( v ) ≥ s d o m ( w ) 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) = 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) = s d o m ( u )
证明: 根据引理 10 我们知道 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) 𝑑 𝑜 𝑚 𝑢 s d o m ( u ) d o m u
考虑任意一条 𝑠 s 𝑢 u 𝑃 P 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑃 P 𝑣 v 𝑃 P 𝑣 < 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) v < s d o m ( u ) 𝑣 v 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) = 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) = 𝑠 s d o m ( u ) = i d o m ( u ) = s 𝑤 w 𝑃 P 𝑣 v 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑢 u
我们接下来证明 𝑠 𝑑 𝑜 𝑚 ( 𝑤 ) ≤ 𝑣 < 𝑠 𝑑 𝑜 𝑚 ( 𝑣 ) s d o m ( w ) ≤ v < s d o m ( v ) 𝑇 T 𝑣 v 𝑤 w 𝑣 = 𝑣 0 → … 𝑣 𝑘 = 𝑤 v = v 0 → … v k = w 𝑖 ∈ [ 1 , 𝑘 − 1 ] , 𝑣 𝑖 < 𝑤 i ∈ [ 1 , k − 1 ] , v i < w 𝑗 ∈ [ 𝑖 , 𝑘 − 1 ] j ∈ [ i , k − 1 ] 𝑣 𝑗 v j 𝑤 w 𝑣 v 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) ≤ 𝑣 𝑗 s d o m ( u ) ≤ v j 𝑣 𝑗 v j 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑢 u 𝑤 w 𝑠 𝑑 𝑜 𝑚 ( 𝑤 ) ≤ 𝑣 < 𝑠 𝑑 𝑜 𝑚 ( 𝑣 ) s d o m ( w ) ≤ v < s d o m ( v ) 𝑦 = 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) y = s d o m ( u ) 𝑃 P 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u )
定理 3: 对于任意节点 𝑢 u 𝑇 T 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑢 u 𝑣 v 𝑠 𝑑 𝑜 𝑚 ( 𝑣 ) ≤ 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( v ) ≤ s d o m ( u ) 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) = 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( v ) = i d o m ( u )
证明: 考虑到 𝑢 u 𝑣 v 𝑠 𝑑 𝑜 𝑚 ( 𝑣 ) ≤ 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( v ) ≤ s d o m ( u )
由于 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) 𝑣 v 𝑇 T 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u ) 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) i d o m ( v ) 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) i d o m ( v ) 𝑢 u
考虑任意一条 𝑠 s 𝑢 u 𝑃 P 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑃 P 𝑥 x 𝑃 P 𝑥 < 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) x < s d o m ( u ) 𝑥 x 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) = 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) = 𝑠 s d o m ( u ) = i d o m ( u ) = s 𝑦 y 𝑃 P 𝑥 x 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑢 u
与定理 2 的证明过程同理,我们可以得到 𝑠 𝑑 𝑜 𝑚 ( 𝑦 ) ≤ 𝑥 s d o m ( y ) ≤ x 𝑠 𝑑 𝑜 𝑚 ( 𝑦 ) ≤ 𝑥 < 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) ≤ 𝑠 𝑑 𝑜 𝑚 ( 𝑣 ) s d o m ( y ) ≤ x < i d o m ( v ) ≤ s d o m ( v ) 𝑣 v 𝑦 y 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑦 y 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) i d o m ( v ) 𝑣 v 𝑠 s 𝑠 𝑑 𝑜 𝑚 ( 𝑦 ) s d o m ( y ) 𝑦 y 𝑣 v 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) i d o m ( v ) 𝑦 = 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) y = i d o m ( v ) 𝑃 P 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) i d o m ( v )
根据以上两个定理我们能够得到 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) i d o m ( u )
令 𝑣 v 𝑣 v 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) s d o m ( u ) 𝑢 u 𝑠 𝑑 𝑜 𝑚 ( 𝑣 ) s d o m ( v )
𝑖 𝑑 𝑜 𝑚 ( 𝑢 ) = { 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) , i f 𝑠 𝑑 𝑜 𝑚 ( 𝑢 ) = 𝑠 𝑑 𝑜 𝑚 ( 𝑣 ) 𝑖 𝑑 𝑜 𝑚 ( 𝑣 ) , o t h e r w i s e i d o m ( u ) = { s d o m ( u ) , if s d o m ( u ) = s d o m ( v ) i d o m ( v ) , otherwise 只要对上面求解半支配点的代码稍作修改即可.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80 struct E {
int v , x ;
} e [ MAX * 4 ];
int h [ 3 ][ MAX * 2 ];
int dfc , tot , n , m , u , v ;
int fa [ MAX ], fth [ MAX ], pos [ MAX ], mn [ MAX ], idm [ MAX ], sdm [ MAX ], dfn [ MAX ],
ans [ MAX ];
void add ( int x , int u , int v ) {
e [ ++ tot ] = { v , h [ x ][ u ]};
h [ x ][ u ] = tot ;
}
void dfs ( int u ) {
dfn [ u ] = ++ dfc ;
pos [ dfc ] = u ;
for ( int i = h [ 0 ][ u ]; i ; i = e [ i ]. x ) {
int v = e [ i ]. v ;
if ( ! dfn [ v ]) {
dfs ( v );
fth [ v ] = u ;
}
}
}
int find ( int x ) {
if ( fa [ x ] == x ) {
return x ;
}
int tmp = fa [ x ];
fa [ x ] = find ( fa [ x ]);
if ( dfn [ sdm [ mn [ tmp ]]] < dfn [ sdm [ mn [ x ]]]) {
mn [ x ] = mn [ tmp ];
}
return fa [ x ];
}
void tar ( int st ) {
dfs ( st );
for ( int i = 1 ; i <= n ; ++ i ) {
fa [ i ] = sdm [ i ] = mn [ i ] = i ;
}
for ( int i = dfc ; i >= 2 ; -- i ) {
int u = pos [ i ], res = INF ;
for ( int j = h [ 1 ][ u ]; j ; j = e [ j ]. x ) {
int v = e [ j ]. v ;
if ( ! dfn [ v ]) {
continue ;
}
find ( v );
if ( dfn [ v ] < dfn [ u ]) {
res = std :: min ( res , dfn [ v ]);
} else {
res = std :: min ( res , dfn [ sdm [ mn [ v ]]]);
}
}
sdm [ u ] = pos [ res ];
fa [ u ] = fth [ u ];
add ( 2 , sdm [ u ], u );
u = fth [ u ];
for ( int j = h [ 2 ][ u ]; j ; j = e [ j ]. x ) {
int v = e [ j ]. v ;
find ( v );
if ( sdm [ mn [ v ]] == u ) {
idm [ v ] = u ;
} else {
idm [ v ] = mn [ v ];
}
}
h [ 2 ][ u ] = 0 ;
}
for ( int i = 2 ; i <= dfc ; ++ i ) {
int u = pos [ i ];
if ( idm [ u ] != sdm [ u ]) {
idm [ u ] = idm [ idm [ u ]];
}
}
}
例题 可以仅求解支配关系,求解过程中记录各个点支配了多少节点,也可以建出支配树求解每个节点的 size.
这里给出后一种解法的代码.
参考代码 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103 #include <iostream>
using std :: cin ;
using std :: cout ;
constexpr int MAX = 3e5 + 5 ;
constexpr int INF = 0x5ffffff ;
struct E {
int v , x ;
} e [ MAX * 4 ];
int n , m , u , v , tot , dfc ;
int ans [ MAX ], dfn [ MAX ], pos [ MAX ], sdm [ MAX ], idm [ MAX ], fa [ MAX ], mn [ MAX ],
fth [ MAX ];
int h [ 3 ][ MAX * 2 ];
void add ( int x , int u , int v ) {
e [ ++ tot ] = { v , h [ x ][ u ]};
h [ x ][ u ] = tot ;
}
void dfs ( int u ) {
dfn [ u ] = ++ dfc ;
pos [ dfc ] = u ;
for ( int i = h [ 0 ][ u ]; i ; i = e [ i ]. x ) {
int v = e [ i ]. v ;
if ( ! dfn [ v ]) {
dfs ( v );
fth [ v ] = u ;
}
}
}
int find ( int x ) {
if ( fa [ x ] == x ) {
return x ;
}
int tmp = fa [ x ];
fa [ x ] = find ( fa [ x ]);
if ( dfn [ sdm [ mn [ tmp ]]] < dfn [ sdm [ mn [ x ]]]) {
mn [ x ] = mn [ tmp ];
}
return fa [ x ];
}
void tar ( int st ) {
dfs ( st );
for ( int i = 1 ; i <= n ; ++ i ) {
mn [ i ] = fa [ i ] = sdm [ i ] = i ;
}
for ( int i = dfc ; i >= 2 ; -- i ) {
int u = pos [ i ], res = INF ;
for ( int j = h [ 1 ][ u ]; j ; j = e [ j ]. x ) {
int v = e [ j ]. v ;
if ( ! dfn [ v ]) {
continue ;
}
find ( v );
if ( dfn [ v ] < dfn [ u ]) {
res = std :: min ( res , dfn [ v ]);
} else {
res = std :: min ( res , dfn [ sdm [ mn [ v ]]]);
}
}
sdm [ u ] = pos [ res ];
fa [ u ] = fth [ u ];
add ( 2 , sdm [ u ], u );
u = fth [ u ];
for ( int j = h [ 2 ][ u ]; j ; j = e [ j ]. x ) {
int v = e [ j ]. v ;
find ( v );
if ( u == sdm [ mn [ v ]]) {
idm [ v ] = u ;
} else {
idm [ v ] = mn [ v ];
}
}
h [ 2 ][ u ] = 0 ;
}
for ( int i = 2 ; i <= dfc ; ++ i ) {
int u = pos [ i ];
if ( idm [ u ] != sdm [ u ]) {
idm [ u ] = idm [ idm [ u ]];
}
}
for ( int i = dfc ; i >= 2 ; -- i ) {
++ ans [ pos [ i ]];
ans [ idm [ pos [ i ]]] += ans [ pos [ i ]];
}
++ ans [ 1 ];
}
int main () {
cin >> n >> m ;
for ( int i = 1 ; i <= m ; ++ i ) {
cin >> u >> v ;
add ( 0 , u , v );
add ( 1 , v , u );
}
tar ( 1 );
for ( int i = 1 ; i <= n ; ++ i ) {
cout << ans [ i ] << ' ' ;
}
}
在 DAG 上求支配树然后求节点 size 即可.
参考代码 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102 #include <iostream>
#include <stack>
#include <vector>
using std :: cin ;
using std :: cout ;
using std :: stack ;
using std :: vector ;
constexpr int MAX = 65536 ;
int n , x , tot ;
int d [ MAX ], w [ MAX ], siz [ MAX ], p [ MAX ], f [ MAX ][ 17 ];
vector < int > e [ MAX ], g [ MAX ], h [ MAX ];
stack < int > s ;
void topo () {
s . push ( 0 );
for ( int i = 1 ; i <= n ; ++ i ) {
if ( ! w [ i ]) {
e [ 0 ]. push_back ( i );
g [ i ]. push_back ( 0 );
++ w [ i ];
}
}
while ( ! s . empty ()) {
int x = s . top ();
s . pop ();
p [ ++ tot ] = x ;
for ( int i : e [ x ]) {
-- w [ i ];
if ( ! w [ i ]) {
s . push ( i );
}
}
}
}
int lca ( int u , int v ) {
if ( d [ u ] < d [ v ]) {
std :: swap ( u , v );
}
for ( int i = 15 ; i >= 0 ; -- i ) {
if ( d [ f [ u ][ i ]] >= d [ v ]) {
u = f [ u ][ i ];
}
}
if ( u == v ) {
return u ;
}
for ( int i = 15 ; i >= 0 ; -- i ) {
if ( f [ u ][ i ] != f [ v ][ i ]) {
u = f [ u ][ i ];
v = f [ v ][ i ];
}
}
return f [ u ][ 0 ];
}
void dfs ( int x ) {
siz [ x ] = 1 ;
for ( int i : h [ x ]) {
dfs ( i );
siz [ x ] += siz [ i ];
}
}
void build () {
for ( int i = 2 ; i <= n + 1 ; ++ i ) {
int x = p [ i ], y = g [ x ][ 0 ];
for ( int j = 1 , q = g [ x ]. size (); j < q ; ++ j ) {
y = lca ( y , g [ x ][ j ]);
}
h [ y ]. push_back ( x );
d [ x ] = d [ y ] + 1 ;
f [ x ][ 0 ] = y ;
for ( int i = 1 ; i <= 15 ; ++ i ) {
f [ x ][ i ] = f [ f [ x ][ i - 1 ]][ i - 1 ];
}
}
}
int main () {
cin >> n ;
for ( int i = 1 ; i <= n ; ++ i ) {
while ( true ) {
cin >> x ;
if ( ! x ) {
break ;
}
e [ x ]. push_back ( i );
g [ i ]. push_back ( x );
++ w [ i ];
}
}
topo ();
build ();
dfs ( 0 );
for ( int i = 1 ; i <= n ; ++ i ) {
cout << siz [ i ] - 1 << '\n' ;
}
return 0 ;
}
2026/1/7 08:56:54 ,更新历史 在 GitHub 上编辑此页! AtomAlpaca , Tiphereth-A , c-forrest , CharlieVinnie , ClConstantine , cyyself , Lampese , tder6 CC BY-SA 4.0 和 SATA